In matematica, un insieme è una collezione di oggetti, che è a sua volta un oggetto. Si tratta di un concetto fondamentale della matematica moderna, a partire dal quale si è sviluppata la teoria degli insiemi. Nell'uso informale gli oggetti della collezione possono essere qualunque cosa: numeri, lettere, persone, figure, etc., anche non necessariamente omogenei; nelle formalizzazioni matematiche gli oggetti della collezione vanno invece ben definiti e determinati. Il concetto di insieme è considerato primitivo ed intuitivo: primitivo perché viene introdotto come nozione non derivabile da concetti più elementari; intuitivo perché viene introdotto come generalizzazione della nozione di insieme finito, che a sua volta è introdotta dall'analogia con l'esperienza sensibile di scatole che contengono oggetti materiali (tendenzialmente omogenei); questa impostazione si basa sulla convinzione che l'idea di insieme sia naturalmente presente nella mente umana.
Gli oggetti che compongono un insieme si dicono elementi di questo insieme; nel linguaggio matematico, detto a un elemento dell'insieme A, si dice che a appartiene ad A o in simboli
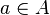. Un insieme A è sottoinsieme di un altro insieme B quando tutti gli elementi di A appartengono anche a B.Ciò che caratterizza il concetto di insieme e lo differenzia da strutture matematiche simili sono essenzialmente le seguenti proprietà:
- un elemento può appartenere o non appartenere a un determinato insieme, non ci sono vie di mezzo (come accade invece per gli insiemi sfocati);
- un elemento non può comparire più di una volta in un insieme (mentre può comparire più volte in un multiinsieme);
- gli elementi di un insieme non hanno un ordine di comparizione (come invece accade alle componenti di un vettore o di una ennupla);
- gli elementi di un insieme lo caratterizzano univocamente: due insiemi coincidono se e solo se hanno gli stessi elementi.
John Venn (Kingston upon Hull, 4 agosto 1834 – Cambridge, 4 aprile 1923) è stato un matematico e statistico inglese, pastore della Chiesa Evangelica, noto nel campo della logica e della teoria della probabilità.
Per quanto riguarda la logica deduttiva Venn ha approfondito i procedimenti logici introdotti da Boole. Egli inoltre riteneva che la logica simbolica (termine tra l'altro da lui coniato) non fosse per forza di cose in contrasto con il ragionamento tipico del senso comune.
...
Leonhard Euler, noto in Italia come Eulero (Basilea, 15 aprile 1707 – San Pietroburgo, 18 settembre 1783), è stato un matematico e fisico svizzero.
È considerato il più importante matematico dell'Illuminismo. È noto per essere tra i più prolifici di tutti i tempi e ha fornito contributi storicamente cruciali in svariate aree: analisi infinitesimale, funzioni speciali, meccanica razionale, meccanica celeste, teoria dei numeri, teoria dei grafi. Sembra che Pierre Simon Laplace abbia affermato "Leggete Eulero; egli è il maestro di tutti noi".[1]
Eulero è stato senz'altro il più grande fornitore di "denominazioni matematiche", offrendo il suo nome a una quantità impressionante di formule, teoremi, metodi, criteri, relazioni, equazioni. In geometria: il cerchio, la retta e i punti di Eulero relativi ai triangoli, più la relazione di Eulero, che riguardava il cerchio circoscritto a un triangolo; nella teoria dei numeri: il criterio di Eulero, l'indicatore di Eulero, l'identità di Eulero, la congettura di Eulero; nella meccanica: gli angoli di Eulero, il carico critico di Eulero (per instabilità); nell'analisi: la costante di Eulero-Mascheroni; in logica: il diagramma di Eulero-Venn; nella teoria dei grafi: (di nuovo) la relazione di Eulero; nell'algebra: il metodo di Eulero (relativo alla soluzione delle equazioni di quarto grado); nel calcolo differenziale: il metodo di Eulero (riguardante le equazioni differenziali).
Sempre a Eulero si legano altri oggetti matematici, attraverso l'aggettivo "euleriano", quali: il ciclo euleriano, il grafo euleriano, la funzione euleriana di prima specie o funzione beta, e quella di seconda specie o funzione gamma, la catena euleriana di un grafo senza anse, i numeri euleriani (differenti dai Numeri di Eulero).
Anche se fu prevalentemente un matematico diede importanti contributi alla fisica e in particolare alla meccanica classica e celeste. Per esempio sviluppò l'equazione delle travi di Eulero-Bernoulli e le equazioni di Eulero-Lagrange. Inoltre determinò le orbite di molte comete.
Eulero tenne contatti con numerosi matematici del suo tempo; in particolare tenne una lunga corrispondenza con Christian Goldbach confrontando con lui alcuni dei propri risultati. Egli inoltre seppe coordinare il lavoro di altri matematici che gli furono vicini: i figli Johann Albrecht Euler e Christoph Euler, i membri dell'Accademia di San Pietroburgo W. L. Krafft e Anders Johan Lexell e il suo segretario Nicolaus Fuss (che era anche il marito di sua nipote); a tutti i collaboratori riconobbe i meriti.
Complessivamente esistono 886 pubblicazioni di Eulero. Buona parte della simbologia matematica tuttora in uso venne introdotta da Eulero, per esempio i per i numeri immaginari, Σ come simbolo per la sommatoria, f(x) per indicare una funzione. Diffuse l'uso della lettera π per indicare pi greco.
...
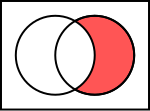
Un diagramma di Eulero-Venn (o semplicemente diagramma di Venn) è la rappresentazione grafica di un insieme che consiste nel racchiuderne gli elementi all’interno di una linea curva chiusa non intrecciata.
Gli elementi dell'insieme vengono evidenziati con punti interni alla linea e son scritti con lettere minuscole, gli elementi che non appartengono all’insieme con punti esterni ad essa.
Più precisamente possiamo asserire che un "diagramma di Venn" è un particolare tipo di grafico utilizzato per rappresentare un'algebra degli insiemi.
Seguendo regole specifiche, in questo tipo di grafico possiamo presentare degli elementi, degli insiemi, l'universo algebrico e le eventuali relazioni che possono esistere fra elementi o fra insiemi:
- gli elementi sono rappresentati sotto forma di punti affiancati da una lettera alfabetica minuscola per associarvi un nome simbolico
- per rappresentare un insieme si usa una linea chiusa affiancata da una lettera alfabetica maiuscola che denota il nome di quell'"insieme"
- ogni possibile relazione tra elementi dello stesso insieme o di insiemi diversi verrà indicata tramite un archetto che indica fra quali elementi sussiste la relazione.
Insiemi numerici
- L'insieme
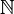dei numeri naturali - L'insieme
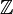dei numeri interi - L'insieme
dei numeri razionali - L'insieme
dei numeri reali - L'insieme
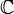dei numeri complessi - L'insieme
dei quaternioni
La teoria degli insiemi svolge un ruolo importante per i fondamenti della matematica e si colloca nell'ambito della logica matematica. Prima della metà del sec. XIX la nozione di insieme veniva considerata solo come qualcosa di intuitivo e generico. Essa è stata inizialmente sviluppata nella seconda metà del XIX secolo dal matematico tedesco Georg Cantor, è stata al centro dei dibattiti sui fondamenti dal 1890 al 1930 ed ha ricevuto le prime sistemazioni assiomatiche per merito di Ernst Zermelo, Adolf Fraenkel, Paul Bernays, Kurt Gödel, John von Neumann e Thoralf Skolem, e le convenzioni linguistico-formali col contributo di Gottlob Frege (quantificatore universale ed esistenziale) e Giuseppe Peano (notazione e sintassi). In questo periodo si sono assestati due sistemi di assiomi chiamati rispettivamente sistema assiomatico di Zermelo-Fraenkel e sistema assiomatico di Von Neumann-Bernays-Gödel.
Successivamente si sono affrontate le tematiche riguardanti il problema della completezza dei sistemi di assiomi (v. teorema di incompletezza di Gödel), i rapporti con la teoria della calcolabilità (v.a. macchina di Turing) e la compatibilità dei sistemi di assiomi con l'assioma della scelta e con assiomi equivalenti o simili.
Accanto a differenti consolidate teorie formali degli insiemi (vedi anche teoria assiomatica degli insiemi) esistono esposizioni più intuitive che costituiscono la cosiddetta teoria naïve degli insiemi.
...
La teoria ingenua degli insiemi venne creata alla fine del XIX secolo da Georg Cantor allo scopo di permettere ai matematici di lavorare in modo consistente con gli insiemi infiniti.
Come si scoprì più tardi, l'assunzione che sia possibile eseguire qualsiasi operazione sugli insiemi senza restrizioni porta a antinomie come il paradosso di Russell. In risposta, la teoria assiomatica degli insiemi fu sviluppata per determinare precisamente quali operazioni sono ammesse e quando. Oggi, quando i matematici parlano di "teoria degli insiemi" come campo di studio, in genere intendono la teoria assiomatica degli insiemi, ma quando parlano di teoria degli insiemi come semplice strumento da applicare in altri campi della matematica, intendono solitamente la teoria ingenua degli insiemi.
La teoria assiomatica degli insiemi può essere piuttosto astrusa e ha poca influenza sulla matematica ordinaria. Quindi è utile studiare gli insiemi nell'originale senso ingenuo allo scopo di sviluppare abilità nel lavorare con essi. Inoltre, una buona padronanza della teoria ingenua degli insiemi è necessaria come prima fase nella comprensione della motivazione per la teoria assiomatica.
...
Dal punto di vista più generale, la teoria dei tipi è la branca della matematica e della logica che si occupa di classificare generiche entità, raggruppandole in collezioni chiamate tipi. Sotto questo punto di vista vi sono punti di contatto con la nozione di tipo della metafisica. La moderna formulazione della teoria dei tipi è, in parte, nata dal tentativo di dare una risposta al cosiddetto Paradosso di Russell, ed è estesamente trattata nei Principia Mathematica di Bertrand Russell e Alfred North Whitehead.
Con la diffusione di computer sempre più potenti, e l'introduzione di linguaggi di programmazione per lo sviluppo di programmi, la teoria dei tipi ha trovato un significativo campo di applicazione, soprattutto nell'ambito della progettazione degli stessi linguaggi di programmazione. In questo contesto, esistono diverse definizioni applicabili a un sistema dei tipi, ma la seguente, dovuta a Benjamin C. Pierce è probabilmente quella che raccoglie il maggiore consenso:
- "Un sistema di tipi è un metodo sintattico trattabile,
in grado di dimostrare l'assenza di determinati comportamenti nei
programmi mediante la classificazione di espressioni fatta in base alla
natura dei valori che esse elaborano."
- (Types and Programming Languages, MIT Press, 2002)
Per esempio, supponiamo che un sistema di tipi classifichi il valore
ciao come stringa e il valore 5 come intero e, sulla base di tali diverse assegnazioni, proibisca al programmatore di sommare ciao a 5. All'interno di questo sistema, sarebbe "illegale" l'istruzione di programma:ciao+5
La progettazione e l'implementazione di un sistema di tipi è un argomento vasto e complesso, quasi come lo stesso linguaggio di programmazione che lo utilizza. Gli ideatori e gli studiosi dei sistemi di tipi si spingono ad affermare che si tratta dell'essenza stessa del linguaggio:
- "Progettate correttamente il sistema dei tipi e vedrete che il linguaggio si progetterà da sé!"
Nessun commento:
Posta un commento
Salve, donatemi un pò dei Vostri Pensieri: